tmuxのpopupを使ってターミナル画面でClaude Codeと棲み分ける
Claude CodeをはじめとするCLI型のコーディングエージェントはターミナル画面中の一定領域を占有します。
元々自分は、ターミナルマルチプレクサであるtmuxを利用していて、リポジトリをプロジェクトとみなし、一つのウィンドウを対応させ、その中でペインを分ける構成をとっていました。 その配置と各ペインのサイズのなかで、エージェントの入る余地はなく、どうしてもペイン内で共有させるか、異なるウィンドウを割り当てる必要がありました。 しかしながら、役割を共有させたペインの裏側や異なるウィンドウに散らばったエージェントのセッションを探し回るのは非常に面倒に感じていました。
そんな中、以下のtmux popupの活用記事がしっくりきたので、参考にさせてもらいました。
利用の様子
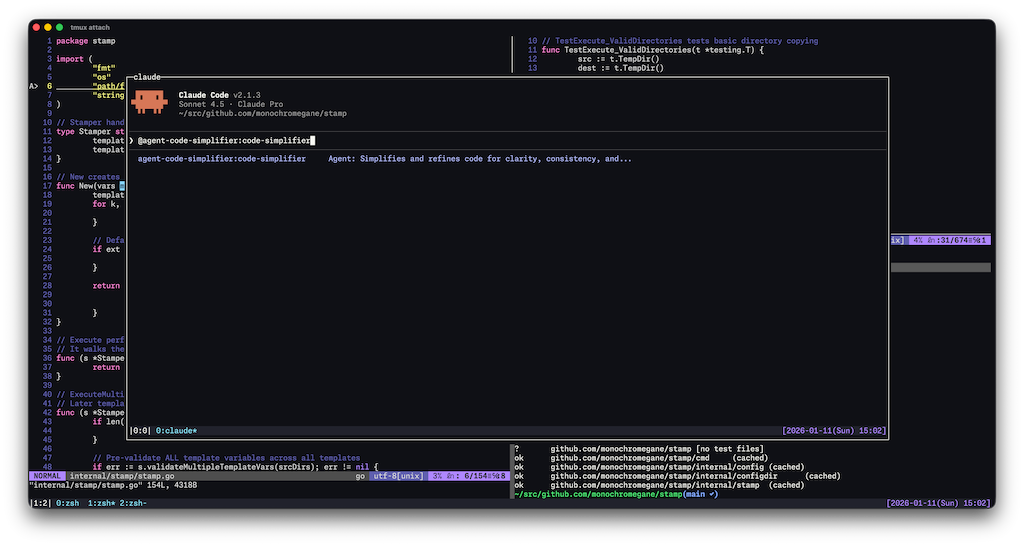
画面の中央の前面領域がtmux popupでClaude Codeを動かしている箇所です。 このpopupの表示・非表示を指定したキーバインドで瞬時にトグルできる体験が非常に良いです。 トグルの様子は、上記の記事のデモが分かりやすいのでぜひご覧いただきたいです。
特に、tmuxのセッションのdetachとattachを行うため、popupを隠しても処理が継続され、ターミナル領域をお気に入りの配置のままコードの確認などが快適に行えるのが非常に有用です。 また、以下の設定で見ていただける通り、tmux側のpopupやキーバインドを使うため、操作中のClaude Codeに干渉しない点もポイントが高いです。
(余談ですがIS_DEMO環境変数をつけてClaude Codeを起動すると組織名やメールアドレスが非表示になってこういうスクリーンショットの時に便利です)
実際の設定
上記の記事はfishだったのでzshで使うために以下のようにしました。
functions/_tmuxpopupでカレントディレクトリ(リポジトリ名)をベースにセッション名を組み立て、セッションがなければ作成、あればattachとdetachをトグルできるようにしています。
セッション名の組み立てのところを自分の環境に合わせると使いまわせると思います。
function _tmuxpopup() {
local initial_cmd="${1:-}"
local title="${2:-}"
local width='80%'
local height='80%'
local session
session="$(tmux display-message -p -F '#{session_name}' 2>/dev/null)" || return 1
local pane_path
pane_path="$(tmux display-message -p -F '#{pane_current_path}')" || return 1
local home_src="${HOME}/src"
local key=""
if [[ "$pane_path" == ${home_src}/*/*/*(|/*) ]]; then
local rest="${pane_path#${home_src}/}"
local parts=(${(s:/:)rest})
local org="${parts[2]}"
local repo="${parts[3]}"
repo="${repo%-wt}"
key="${org}/${repo}"
else
key="${pane_path:t}"
fi
local safe_key="${key//\//_}"
safe_key="${safe_key//[^A-Za-z0-9_.-]/_}"
local popup_session="popup_${title}_${safe_key}"
if [[ "$session" == popup_* ]]; then
tmux detach-client
return 0
fi
local exec_cmd
if [[ -n "$initial_cmd" ]]; then
exec_cmd="tmux attach -t ${popup_session} || tmux new -s ${popup_session} '${initial_cmd}'"
else
exec_cmd="tmux attach -t ${popup_session} || tmux new -s ${popup_session}"
fi
tmux display-popup \
-d "#{pane_current_path}" \
-xC -yC \
-w "$width" -h "$height" \
-T "$title" \
-E "$exec_cmd"
}
上記の関数はpopup時に起動したいコマンドとpopupのタイトルを受け付けられる共通関数なので、Claude Codeを立ち上げるため具体的な実装をfunctions/_tmuxpopup-claudeに記述しました。
function _tmuxpopup-claude() {
_tmuxpopup "claude" "claude"
}
上記の関数たちを.zshrcでautoloadしておきます。これでこの関数がいつでも呼び出せるようになります。
autoload -Uz _tmuxpopup
autoload -Uz _tmuxpopup-claude
実際の呼び出しはコマンドではなくtmux.confにキーバインドとして登録しておきます。こうすることで、popup内のClaude Code起動中でもpopupをいつでも隠すことができます。
bind , run-shell 'zsh -ic "_tmuxpopup-claude"'
これでprefix + ‘,‘でpopupをトグルできるようになりました。非常に快適です。
並列実行
これだけだと再紹介にしかならないので、並列実行のために試しているものも紹介しておきます。
ccmanagerはClaude Codeをはじめとするコーディングエージェントの並列実行を管理するためのツールです。 エージェント単位でgit worktreeを割り当てることができるので、並列実行時のコンフリクトなども回避することができます。
上で紹介した_tmuxpopupは起動したいコマンドを差し替えるだけで使えるのでccmanagerを呼ぶようにするだけで良いです。
function _tmuxpopup-ccmanager() {
_tmuxpopup "ccmanager" "ccmanager"
}
これでプロジェクトごとの並列実行はかなり便利になりますが、いわゆる承認疲れの現象が発生するため、ある程度の権限を持たせた上で安全に実行したくなります。 そこで、Dev Containerと組み合わせます。 幸い、ccmanagerはDev Containerの利用も視野に入れているようで、探すと専用のオプションがあります。 それを踏まえて、先の関数を以下のように変更できます。
function _tmuxpopup-ccmanager() {
_tmuxpopup \
'ccmanager --devc-up-command "devcontainer up --docker-path podman --workspace-folder ." --devc-exec-command "devcontainer exec --docker-path podman --workspace-folder ."' \
'ccmanager'
}
podmanを使う場合のオプションが含まれているので環境に応じて適宜読み替えていただければと思います。
また、予めDev Container CLIもインストールしておく必要があります。
これで、プロジェクトのDev Containerの設定(.devcontainerディレクトリ)を使ってccmanagerがよしなにやってくれます。
なお、コンテナ内にClaude Codeが含まれる必要があるため、Dev Container Featuresなどで追加しておくと良いです。
以下のように設定し、Claude Codeのpopupと使い分けることができます。
bind . run-shell 'zsh -ic "_tmuxpopup-ccmanager"'
おわりに
tmux popupを使うことでClaude Codeとターミナル領域をうまく棲み分けることができて非常に快適になりました。 しかしながら、並列実行の部分は実はまだ試行錯誤中です。 特に、Dev Container + git worktree + Claude Codeの相性はあまり良くないと思っていて、マウント周りを工夫する必要があり、なかなか全てのリポジトリで気軽に使えてないのが現状です。 また、Dev Containerであれローカルであれ、単純に自分が起点にエージェントとやりとりする構造から逆転させないと目指す並列は近づけないなあとも思っているので、引き続き試行錯誤していきたいと思います。



