THINKING MEGANE

待ち行列理論に使われる分布に従う乱数をGo言語で生成する

待ち行列理論をシミュレーションする際にいくつかの分布に従う乱数を生成する必要があったのでメモ． また，確率まわりの用語と分布についても理解が曖昧な点があったのでこの機会にまとめておく．

用語の整理

確率

確率は，

\[ \frac{ある事象の起こる場合の数}{全ての事象の起こる場合の数} \]

で求められる．

確率変数

確率変数は，事象に対応した実数のこと． 確率変数には，離散型と連続型の二種類がある． サイコロの出目のようなものは離散型で，身長や体重のような（原理的には）連続の値になるものは連続型．

確率分布

確率分布は確率と確率変数との対応付け． そもそも辞書的な意味での「分布」は「粗密の程度を含めた，空間的な広がり具合」を表す． 度数分布では階級と度数（階級に含まれる変量の数）の対応付けであった． また，これらの分布は，度数分布と同様に確率分布表や確率分布グラフとして表すことができる．

確率を返す関数

ここで，ある確率変数を入力に，対応する確率を出力する関数を考える．

確率質量関数

離散型の確率変数であれば，確率分布表を照会し，対応する確率を得ることができる． 確率変数を入力に，対応する確率を出力する関数を確率質量関数（または確率関数）[1]と言い，サイコロの出目を確率変数$X$とした時に1が出る確率を$P(X=1)=\frac{1}{6}$のように書ける． もちろん確率の総和は1である．

確率密度関数

連続型の確率変数の場合は，ある一点の値を入力とすると対応する確率は常に0となる． これは，ある範囲においても実数は無限個あるため，全事象が無限になることから，確率の定義より$\frac{1}{\infty}=0$となるためである． このように連続型の確率変数からは直接的に確率を求めることができないので，この連続型の確率変数を対応する「何か」に変換する必要がある． また，その「何か」は確率に変換できる必要がある． 確率の定義から，総和は1である． また，連続型の確率変数であることから，和は積分で求めることになる．

連続型の確率変数をx軸に，この連続型の確率変数を対応する「何か」をy軸にプロットした時に，ある範囲の割合は該当範囲の定積分によって導くことができる． そして，全体の積分が1で，その中のある範囲の定積分が，事象がその範囲に含まれる確率に従うような「何か」があれば，それを連続型の確率変数の確率に用いることができる． そのような「何か」が存在するとき，「何か」は「確率密度」と呼ばれ，連続型の確率変数を入力とし，確率密度を出力する関数を「確率密度関数」と呼ばれる[2]．

このとき，確率密度関数$f(x)$に従う確率変数$X$が$(a \leqq X \leqq b)$となる確率は\[\int_a^b f(x) dx\]のように書ける．

確率密度は，その確率変数の相対的な発生のしやすさを表すに過ぎないので，部分的にy軸(確率密度関数の返す値)が1を超えても構わない（全体の面積として1になれば良い．例えば，確率密度関数が$f(x)=2x (0 \leqq X \leqq 1)$のときなど）．

待ち行列理論で使う分布

待ち行列理論では待ち行列のモデルの構造を以下のようなケンドール記号を用いて記述する．

  • X/Y/S(N)

ここでXは到着過程の種類，Yはサービス過程の種類，Sは窓口数，Nは待ち行列の長さの制限数が入る． 過程の種類は以下の通り．

種類 説明 備考
M マルコフ過程 到着過程ならポアソン分布，サービス過程なら指数分布
D 確定分布 到着間隔やサービス時間が一定
G 一般の分布 平均値と分散が既知の任意の分布
$E_k$ アーラン分布 k個の指数分布の和の分布

ポアソン分布

単位時間に平均$\lambda$回起きる事象が単位時間に$k$回発生する分布[3]．

平均が$\lambda$のポアソン分布を表す確率質量関数は\[P(X=k)=\frac{\lambda^{k}}{k!}\cdot e^{-\lambda}\]であり平均$E[X]$は$\lambda$となる．

指数分布

平均$\theta$時間に一回発生する事象の発生間隔を表す分布[4]．

平均が$\theta$の指数分布を表す確率密度関数は\[f(x)=\frac{1}{\theta}e^{-\frac{x}{\theta}} (x \geqq 0)\]であり平均$E[X]$は$\theta$となる．

待ち行列とマルコフ過程

あるランダムに起きる事象を発生回数から見たのがポアソン分布，発生間隔(または時間)から見たのが指数関数とみなすことができる． マルコフ過程は未来の挙動は過去の挙動とは無関係であるとする性質を持つ確率過程であり，これらの分布が適合するため利用されている．

単位時間に$\lambda$回到着するとした到着過程はポアソン分布が利用されるが，シミュレーションにおいては平均到着間隔を知りたい． この場合は，$\frac{1}{\lambda}$を到着間隔とした指数分布で求めることができる（1時間に平均5人くる場合，平均1/5時間(12分)の間隔で到着する）． つまり，$\theta=\frac{1}{\lambda}$として，確率密度関数は\[f(x)=\lambda e^{-\lambda x} (x \geqq 0)\]であり平均$E[X]$は$\frac{1}{\lambda}$となる．

なお，ポアソン分布と指数分布の関係の理解には[5]が参考になる．このサイトでは時刻$t$を導入したポアソン分布の累積分布関数から指数分布の確率密度関数を導いている．

アーラン分布

まず，ガンマ分布は平均$\theta$時間に一回発生する事象（指数分布）が$k$回発生するまでの時間の分布[6]である． ガンマ分布の$k=1$のとき，指数分布と等しく，$k$が整数の場合にアーラン分布と呼ばれる．

ガンマ分布を表す確率密度関数は\[\frac{1}{\Gamma(k)\theta^{k}}x^{k-1}e^{-x/\theta}\]であり平均$E[x]$は$k\theta$となる．

また，前述のポアソン分布のパラメタから指数分布の確率密度関数を求めたのと同様に，$\theta=\frac{1}{\lambda}$として，確率密度関数は\[\frac{\lambda^k}{\Gamma(k)}x^{k-1}e^{-\lambda x}\]であり平均$E[x]$は$\frac{k}{\lambda}$とも書ける．

ここまで，$k$回の$\theta=1/\lambda$の指数分布を場合を見てきたが，待ち行列理論の書籍においては，$k$回の$\frac{\theta}{k}=\frac{1}{k\lambda}$の指数分布としている場合がある． すなわち，一つのサービス時間$\theta$が$k$個の工程（1工程あたり$\frac{\theta}{k}$）からなるとみなしている． この場合，確率密度関数は\[\frac{(k\lambda)^k}{\Gamma(k)}x^{k-1}e^{-k\lambda x}\]であり平均$E[X]$は$\theta=1/\lambda$となる．

待ち行列理論で使う分布に従う乱数

ここでは，ある分布に従う乱数をGoでの生成する．

指数分布

指数分布に従う乱数はGoの標準パッケージmath/randで提供されている．

func Exponential(rnd *rand.Rand, lambda float64) float64 {
        return rnd.ExpFloat64() / lambda
}

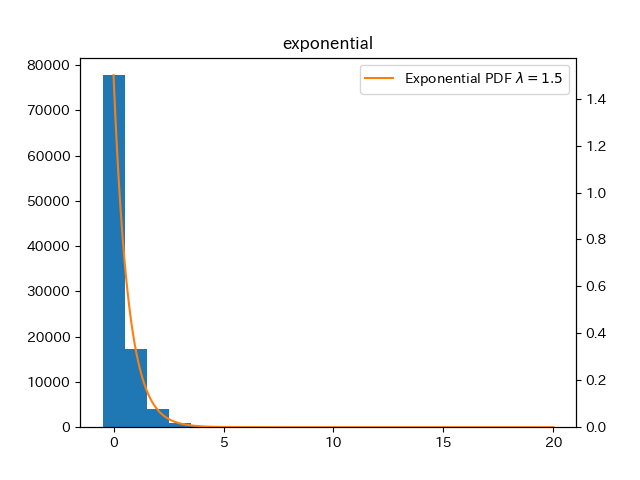
パラメタ$\theta=1/\lambda$に合わせるためには結果を$\lambda$で割る（平均到着率が増えるほど平均到着間隔は狭くなる）．

動作確認のため，生成した乱数のヒストグラムと指数分布の確率密度関数を重ねてプロットした．

hist_and_pdf_exponential

ポアソン分布

ポアソン分布に従う乱数はGoの標準パッケージで提供されていない． そこで指数分布とポアソン分布の関係性を利用して，指数分布で得られた乱数の和が1を超えるまでの最小のカウント数を用いる方法がある[7][8]． 例えば平均到着率($\lambda$)が5人であれば，平均到着間隔($1/\lambda=0.2$)である． ここでカウントは$0.2*5$が平均して得られると考えられる．

func Poisson(rnd *rand.Rand, lambda float64) float64 {
        p := 0.0
        for i := 0; ; i++ {
                p += Exponential(rnd, lambda)
                if p >= 1.0 {
                        return float64(i)
                }
        }
        return 0.0
}

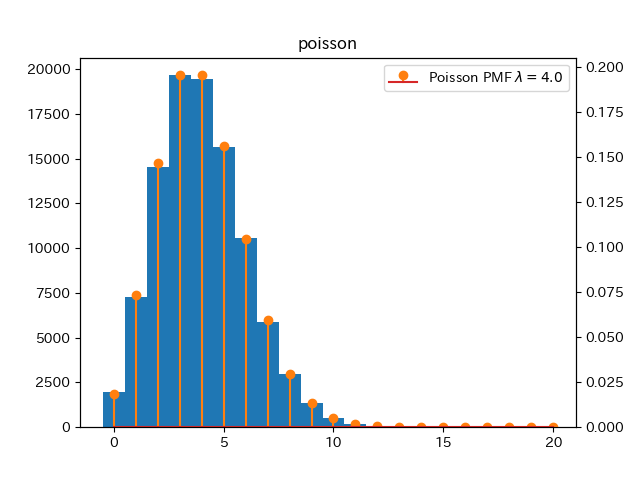
生成した乱数のヒストグラムとポアソン分布の確率質量関数のプロット．

hist_and_pmf_poisson

アーラン分布

アーラン分布もしくはガンマ分布に従う乱数はGoの標準パッケージで提供されていない． しかし，ガンマ分布の定義（k個の指数分布の和の分布）[6]から以下の実装が可能である．

func ErlangKL(rnd *rand.Rand, lambda float64, k int) float64 {
        g := 0.0
        for i := 0; i < k; i++ {
                g += Exponential(rnd, lambda)
        }
        return g
}

ここで，KLは平均が$\frac{k}{\lambda}$であることを表している．

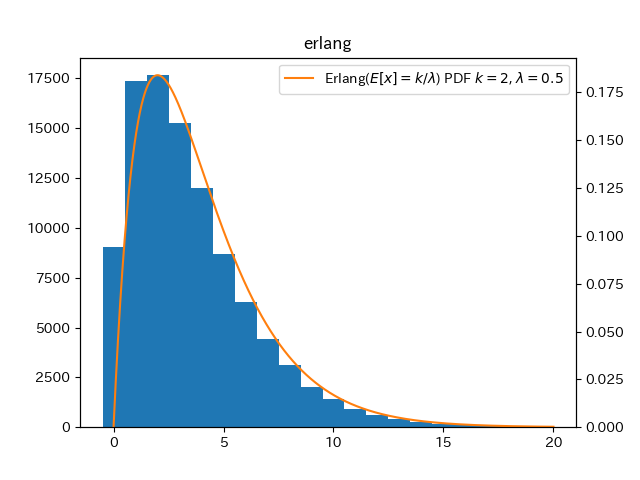
生成した乱数のヒストグラムとアーラン分布の確率密度関数のプロット．

hist_and_pdf_erlangkl

待ち行列理論の参考書にあるようなサービス工程を$k$個に分割するアーラン分布では$k$回の$\frac{\theta}{k}=\frac{1}{k\lambda}$の指数分布となることから以下の実装となる．

func Erlang1L(rnd *rand.Rand, lambda float64, k int) float64 {
        g := 0.0
        for i := 0; i < k; i++ {
                g += Exponential(rnd, float64(k)*lambda)
        }
        return g
}

ここで1Lは平均が$\frac{1}{\lambda}$であることを表している．

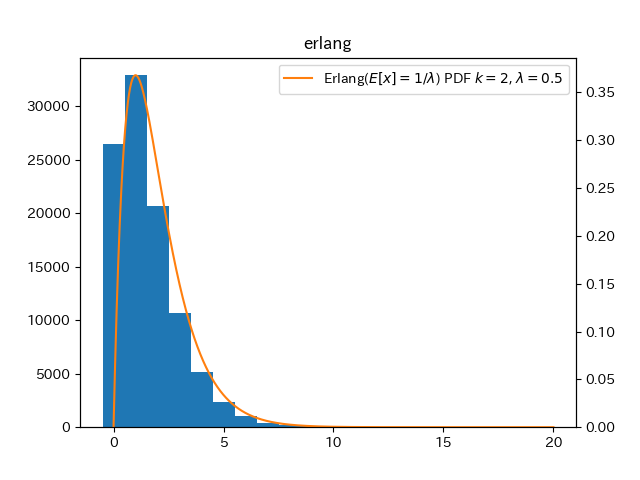
生成した乱数のヒストグラムとアーラン分布の確率密度関数のプロット．

hist_and_pdf_erlang1l

動作確認用のコード

動作確認用のコードは以下にある．

このような感じで利用できる．

go run main.go -size 100000 -dist erlang -e k/l -lambda 0.5 -k 2 > data.txt && python plot.py --dist erlang -e k/l --lambda 0.5 -k 2

参考

このエントリーをはてなブックマークに追加