以前のADWINのように、変化する環境において適応的に振る舞うための仕組みについて調べる中で以下の論文で紹介されていたDynamic Gamma-Poissonモデルについてベイズ推定の理解を兼ねて試してみたのでメモ。

• Agarwal, Deepak, Bee-Chung Chen, and Pradheep Elango. “Spatio-temporal models for estimating click-through rate.” Proceedings of the 18th international conference on World wide web. 2009.

ベイズ推定

統計モデルとは

「ある確率変数$Y$の実現値$y=\{y_1,y_2,..,y_n\}$から、$Y$が本来従う確率分布（真の分布）を推定するためのもの」

とされている。 ベイズ推定はベイズの定理に基づいて観測したデータと過去の情報からデータの本来従う確率分布を推定する。

ベイズの定理 $p(\theta \mid y) \propto p(y \mid \theta)p(y)$ に対して右辺（尤度x事前確率）が具体的な確率値でかつ分布が数え上げられるような単純な場合は理解は比較的容易。

• ベイズ推定の簡単な例と利点

一方で、データの確率分布がパラメタによって変動するような確率質量関数や確率密度関数に従う場合、そのパラメタ（母数）の分布を推定することで、（分布の種類が分かっていればパラメタの推定が分布の特定になるので）データの従う確率分布を推定できる。 この時、データの分布の種類に応じた事前分布を選択することで事後分布が求めやすくなる（共役事前分布）。

このようなパラメタを推定するようなベイズ推定に関しては以下の資料が理解の助けになる。

• ベイズ統計学入門
• ベイズ推定の初歩 二項分布を例に
• Parameter Estimation Fitting Probability Distributions Bayesian Approach

以下、ポアソン分布のパラメタ推定を例にベイズ推定の理解を深め、これを拡張したDynamic Gamma-Poissonモデルを説明する。

ポアソン分布

単位時間に平均$\lambda$回起きる事象が単位時間に$k$回発生する分布。

平均が$\lambda$のポアソン分布を表す確率質量関数は\[P(X=k)=\frac{\lambda^{k}}{k!}\cdot e^{-\lambda}\]であり平均$E[X]$は$\lambda$となる。

ポアソン分布のパラメタ$\lambda$を推定する

Parameter Estimation Fitting Probability Distributions Bayesian Approachのp.19の例を元に説明する。

• $X_1,X_2,..,X_n$ $i.i.d.$ $Poisson(\lambda)$
  • 単位時間に平均$\lambda$回起きる分布に従う確率変数の実現値を$n$回観測
  • $X_i$は0以上の整数値
• $lik(\lambda) = f(x_1, x_2,..,x_n \mid \lambda) = \prod_{i=1}^n f(x_i \mid \lambda)$
  • 尤度はパラメタ$\lambda$において観測した値が得られる確率（この場合は上述したポアソン分布の確率質量関数$P(X=x_i)$）
  • 複数回観測した場合はその同時確率
• $\lambda \sim Gamma(\alpha, \nu)$
  • 事前分布、つまり、$\lambda$が「ある値（の範囲）」を取る確率
  • 今回は事前分布にガンマ分布を仮定する（ポアソン分布の共役事前分布）
  • $\pi(\lambda)$
• $\pi(\lambda \mid x) \propto lik(\lambda) \times \pi(\lambda)$
  • ベイズの定理より事後分布は尤度x事前分布で求められる
  • $P(x\mid\lambda)P(\lambda)$なので、$\lambda$の分布から観測値$x$が得られる確率と言える
• $Gamma(\alpha^*,\nu^*)$ with $\alpha^*=\alpha+\sum_{1}^n x_i$ and $\nu^*=\nu+n$
  • 上を計算すると事後分布は観測された$x$の値の合計を$\alpha$に、観測回数$n$を$\nu$に加えたものをパラメタとするガンマ分布とみなせる
  • 観測したデータから$\lambda$の分布（確率変数が従う確率分布（分布の種類はわかっているのでそのパラメタ））を推定した

Dynamic Gamma-Poissonモデル

論文3.1によれば、クリック数$c$、閲覧数$v$、CTRを$\theta$としたときに、

• 平均$v\theta$(=$\lambda$)である$Poisson(\lambda)$に従い観測されたクリック数から
• $\theta$の事前分布に平均が$\alpha/\gamma$、分散が$\alpha/\gamma^2$である$Gamma(\alpha,\gamma)$を仮定して
• $\theta$の事後分布を$Gamma(\alpha+c,\gamma+v)$として得られるとしている

ただし、実際はこの推定は$\lambda$の推定であるため、CTRとして考えるために以下のように考える。

• $\lambda$を1閲覧($v$)の間の平均回数と考える（つまり$\lambda=1*\theta$）
• 1閲覧に該当する期間を閲覧数分、観測した
• これによって推定された$\lambda$は$\theta$と等しくなる

ここで、$Gamma$のパラメタはこれまでのクリック総数と閲覧総数であることから、$\lambda$の値が変化する場合に過去のデータに引きづられてしまい、速やかな追従を行うことができない。 論文では、Dynamic Gamma-Poissonモデルとして過去の観測結果に対する割引の概念を導入することでこれを解決する。 実現はシンプルで、割引率$(0< \delta \leq1)$を導入し、事後分布を$Gamma(\delta\alpha_{t-1}+c_t,\delta\gamma_{t-1}+v_t)$のように求める。 これによって累積された過去の総数を減らし、直近のデータに重み付けが行われる。 論文中では0.95から1の間ぐらいが良い結果を得たとしている。

以下、実際に同じ条件での$\lambda$の推定を通常のGamma-PoissonモデルとDynamic Gamma-Poissonモデルで行ったものを比較する。 評価では、CTRが0.4のアイテムに対して1ステップごとに7回の閲覧が行われた際のクリック数を観測データとした。 また、20ステップ目にCTRが半分の0.2になっている。

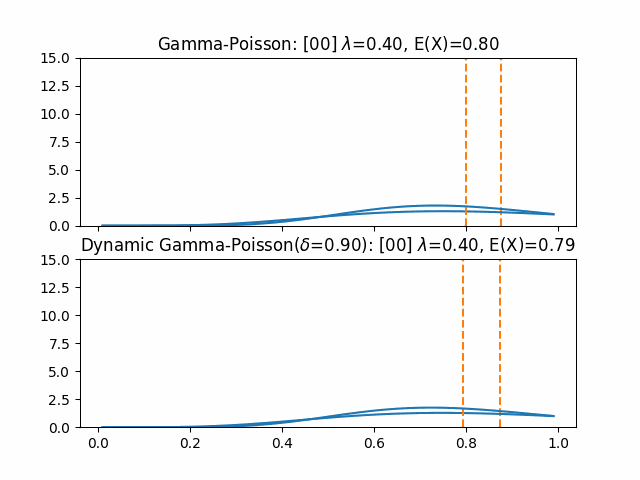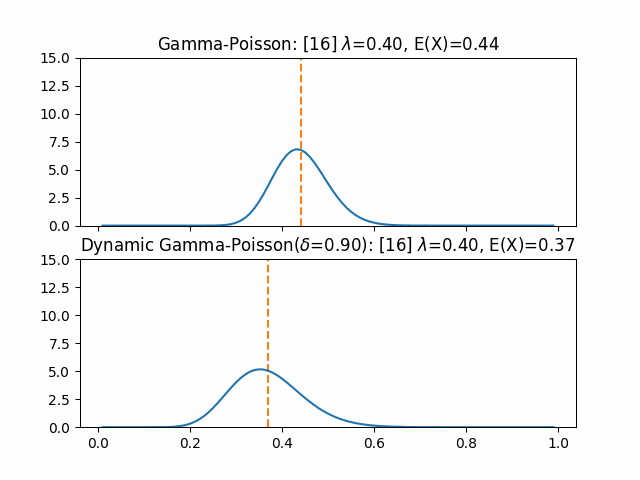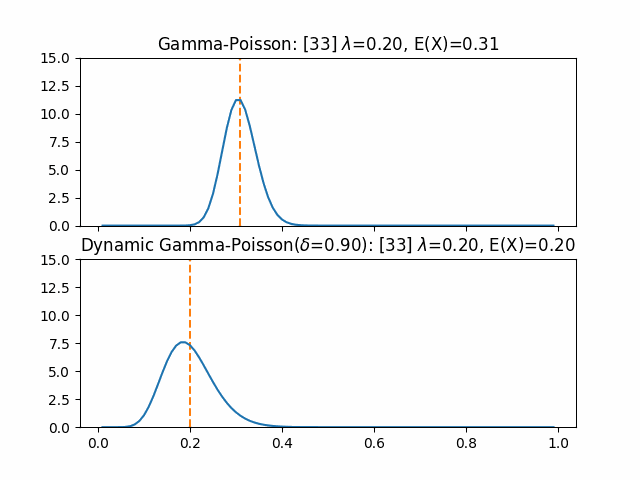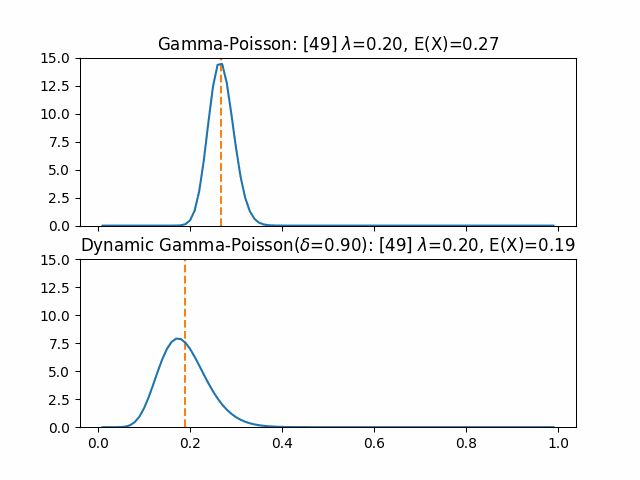
評価期間内では通常の推定の期待値0.3程度までの追従に止まったが、Dynamicな手法ではより早く実際のCTRである0.2に近づけたことが分かる。

動作確認用のコード

動作確認用のコードは以下にある．

• dgp.py

このような感じで利用できる．

python dgp.py --lambda_ 0.4 --view 7 --delta 0.9